Research

Knowledge Diffusion and Reaction Diffusion
The knowledge sharing or diffusion takes place over network structures and this is also a mechanism of network creation – a fundamental aspect of the economic activity. Design framework to study the effect of trade in an endogenous growth model in which comparative advantage and the stock of knowledge are determined by innovation and diffusion. The economic and social importance of knowledge representation dramatically increased to meet the needs of private and business applications for such knowledge diffusion.
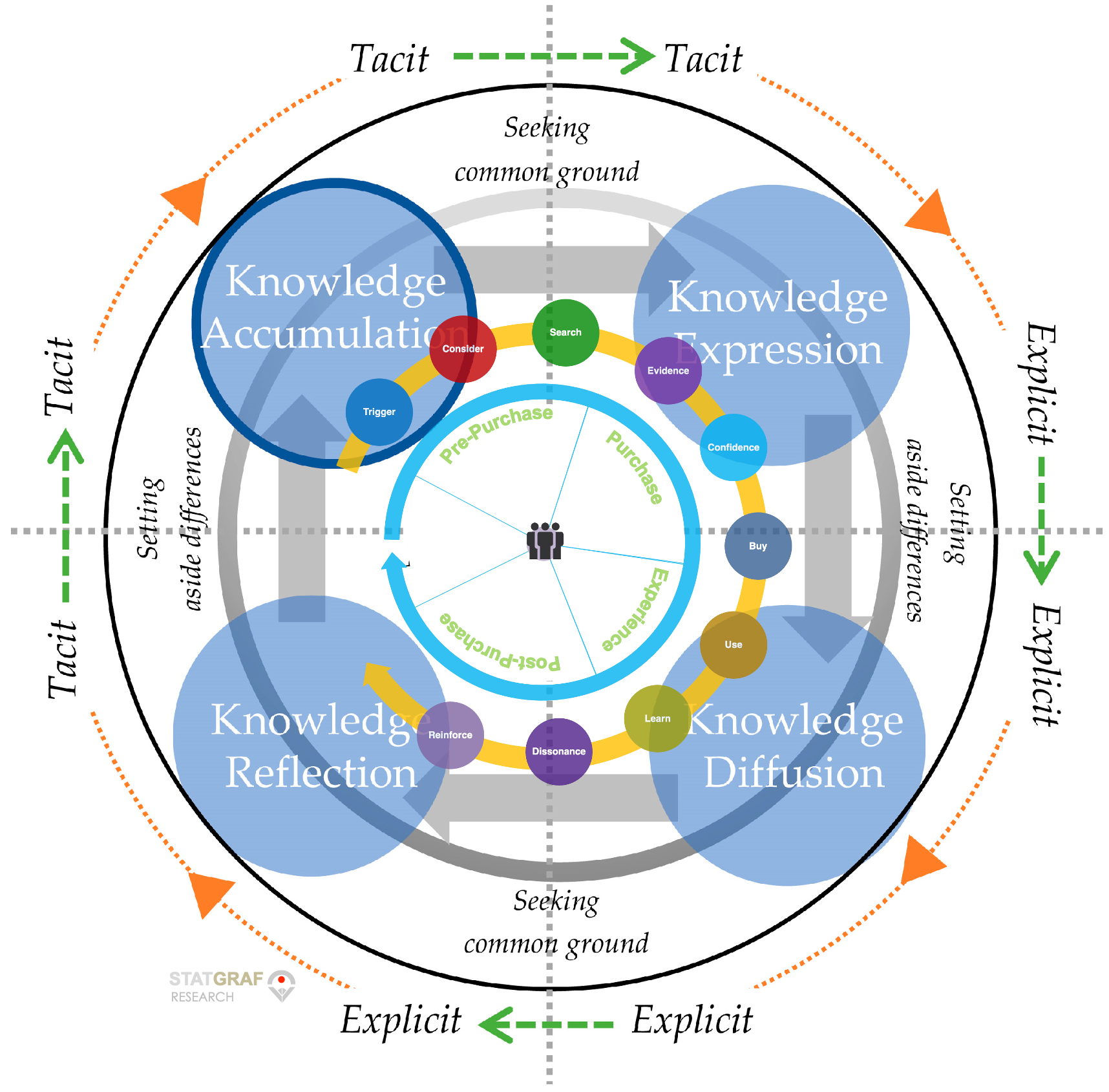
In decision-making, and knowledge diffusion, the process of recognizing features of the situation in which we find ourselves, considering numerous possible alternative responses, selecting and executing one response, observing the outcomes, and adjusting our behavior accordingly.
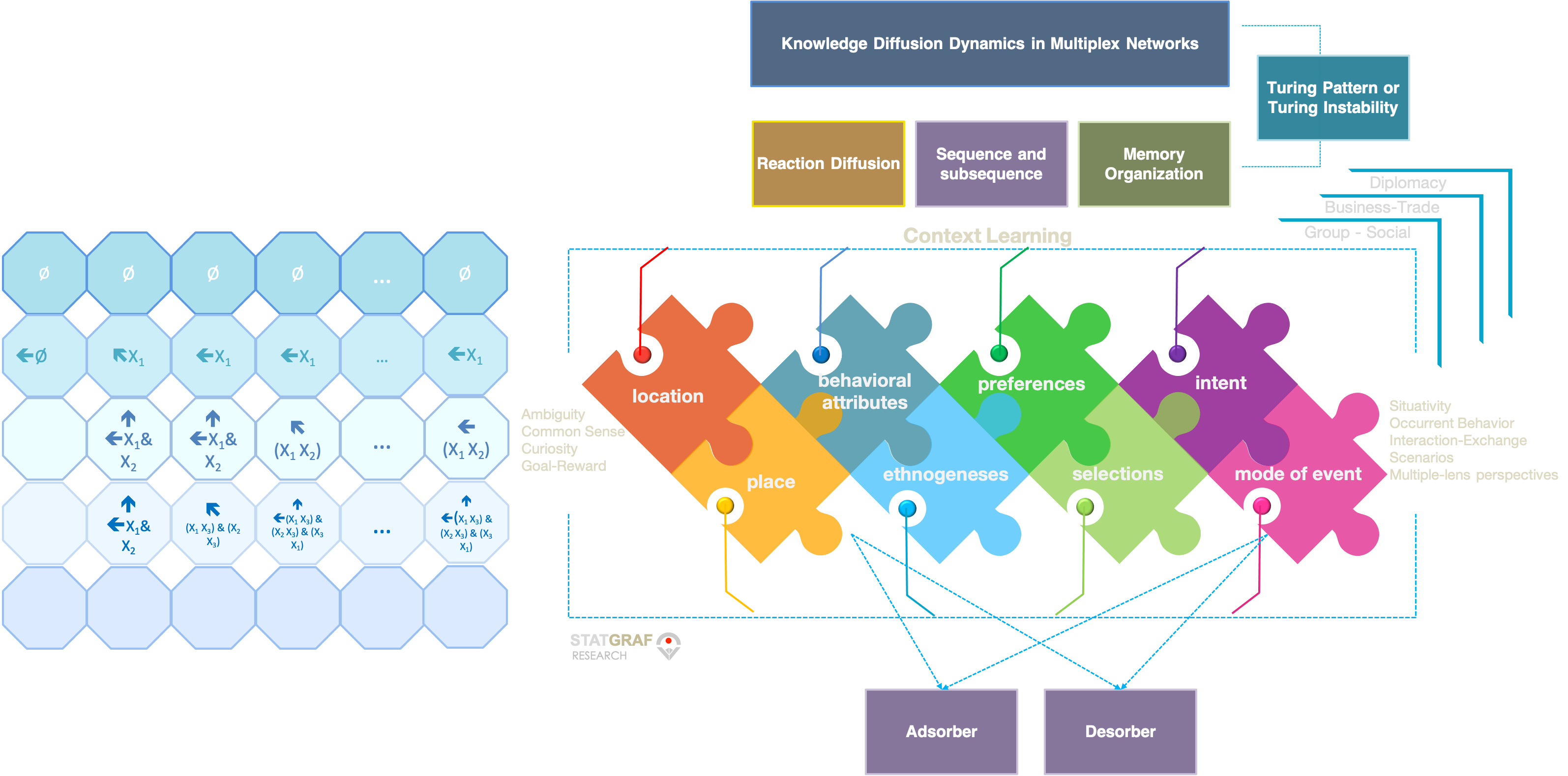
The main paths of the knowledge diffusion network can reveal the important actors and diffusion process, which has an important significance in improving the efficiency of knowledge diffusion. Due to the independent path choice of individual actors (human or machine), knowledge diffusion networks show a dynamic characteristic in collaborative innovation projects.
Our approach to decision-making is through computational models, such as the drift-diffusion model, over multiplex networks, which was originally developed to describe how well-trained participants make rapid decisions between two possible response alternatives. Such computational models impute information about latent cognitive processes based on observable decision-making behavior.
However, both online and offline channels have been adopted for transmitting knowledge in reality, and two channels have some interactions. The spread mechanism of a kind of knowledge in the multiplex networks with consideration of online and offline channels.
First, a knowledge transmission model in the multiplex networks is established and the mean-field equations are derived. Specifically, the transmission rate parameters are tuned to characterize the interaction of knowledge transmission between two channels and the relevance of networks structure is considered in the model.
Then, we obtain the threshold conditions to distinguish whether a kind of knowledge spreads or not among individuals (or subjects) by using two channels. The activity of knowledge exchange between individuals (or subjects) is determined by a knowledge transfer rule that the target node would preferentially select one neighbor node to transfer knowledge with probability p according to their interaction frequency instead of the knowledge distance, otherwise, the target node would build a new link with its second-order neighbor preferentially or select one node in the system randomly with probability 1 − p.
They are one of the most fundamental types of stochastic processes; can be used to model numerous phenomena, including diffusion, interactions, and opinions among humans and animals; and can be used to extract information about important entities or dense groups of entities in a network. Random walks on multiplex networks have been studied for many decades on both regular lattices and on networks with a variety of structures. Additionally, formulated stochastic motion, in the form of ‘‘Brownian motion’’ of users in continuous time due to their collisions with activities and events.
John Hubbard, exploring iterated functions and the infinite fractal wildness of the Mandelbrot set, considered chaos a poor name for his work, because it implied randomness. To him, the overriding message was that simple processes in nature could produce magnificent edifices of complexity without randomness. In nonlinearity and feedback lay all the necessary tools for encoding and then unfolding structures as rich as the human brain.
James Gleick, said in “Chaos: Making a New Science”
Second, set up reaction-diffusion (RD) model, on the other hand, are characterized, as in the chemical systems with two active components that react with other components, and with different diffusion coefficient, to measure feedback and any diffusion-induced instability (Turin-instability). The possibility of pattern formation without pre-pattern is important in both understanding in natural-occurring patterns and synthetic patterns. Reaction-Diffusion (RD) algorithm and implication to subsequent pattern formation in the network are important in the field of non-equilibrium phenomena with relevance to biological and synthetic pattern formation. While homogenous distribution of chemicals was always believed to be a stable state, the symmetry-breaking treatment by Turing on such systems in 1951 showed pattern formation could be more stable in certain cases. This paper reviews the treatment by Turing and the subsequent evidences for and against its application.
Technically, the Hubbard model is an extension of the so-called tight-binding model, wherein electrons can hop between lattice sites without ‘feeling’ each other. In its simplest form, electron hopping can only take place between nearest-neighbour sites, and all hopping processes have the same kinetic energy, −t. The tight-binding model evinces the quantum-mechanical quintessence of electrons in a solid: the emergence of an electronic band structure — intervals of allowed and forbidden energies — lying at the heart of present-day semiconductor technology.
“Disorder is born from the fact that certain elementary entities behave differently from others: some spins try to go in opposite directions; certain atoms are different from most others; certain financial actors sell shares that others are buying; some dinner guests actively dislike others who have been invited and want to sit as far away from them as possible.”
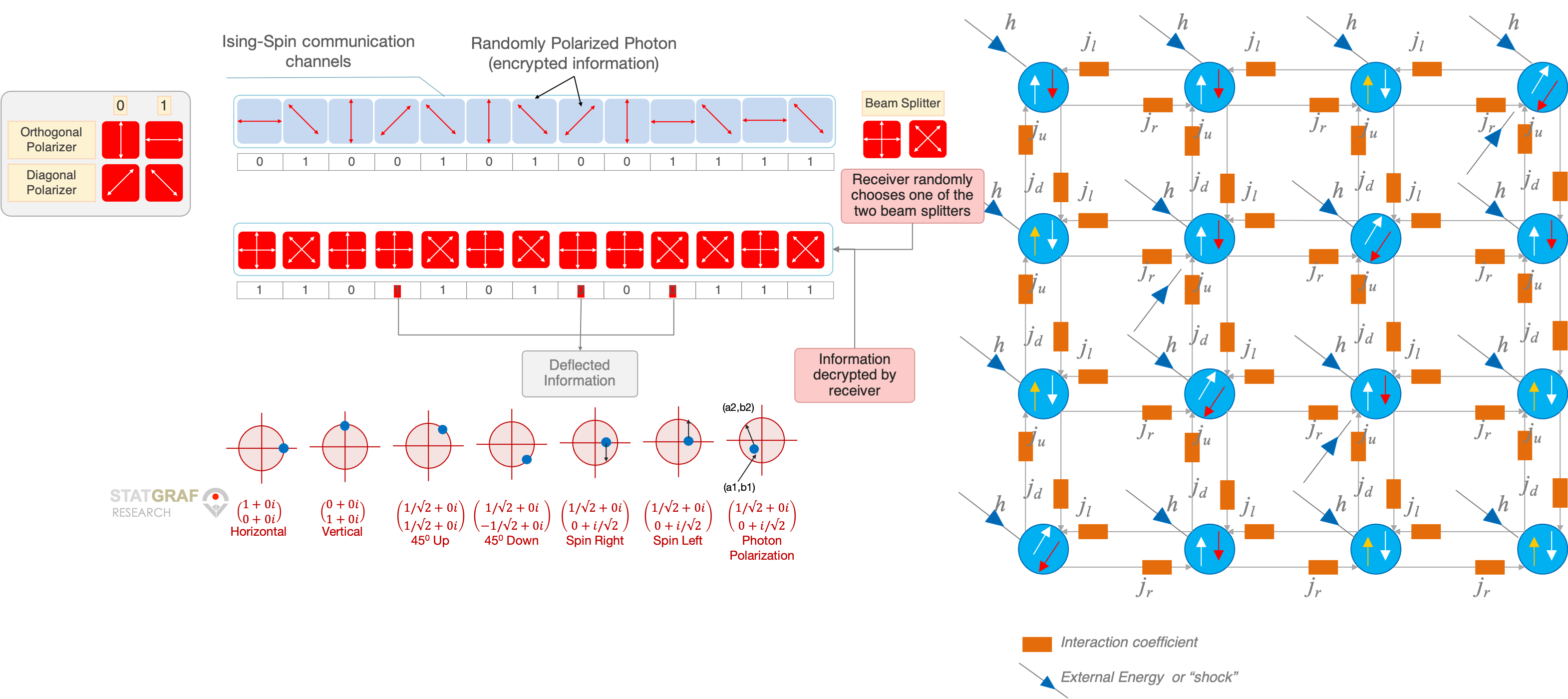
Diffusion in disordered systems does not follow the classical laws which describe transport in ordered crystalline media, and this leads to many anomalous physical properties. Different types of disordered systems exhibiting anomalous diffusion are presented (the incipient infinite percolation cluster, diffusion-limited aggregation clusters, lattice animals, and random combs), and scaling theories as well as numerical simulations of greater sophistication are described. Also, diffusion in the presence of singular distributions of transition rates is discussed and related to anomalous diffusion on disordered structures.
Diffusion processes were among the first dynamics introduced in the context of multiplex networks, where diffusion can occur both within and across layers. In this scenario, flows not only take place through nodes connected at a given layer, but also across two replicas of the same node belonging to two different layers. The fundamental quantity in the study of diffusion is the flux, i.e., the amount of a knowledge which passes near a point in space per unit area per unit time. The SI unit of flux would therefore be molm−2 s−1. Flux is a vector: the best way to think about flux is to imagine a small surface of area A oriented perpendicularly to one of the coordinate axes, say the x axis. The number of moles of the knowledge whose flux along the x axis is Jx entering the volume between the two surfaces per unit time is Jx(x)A, while the number of moles leaving this volume is Jx(x + ∆x)A.
There is well known phenomenon as the diffusion-induced instability or the Turing instability. As a consequence of the Turing instability exhibits spatially inhomogeneous structures called Turing patterns. Therefore, the Turing instability is regarded as important for the onset of pattern formation on the reaction-diffusion systems.
