Research


Holmes goes on to tell Dr. Watson how his reasoning abilities are different than most people…
“Most people, if you describe a train of events to them, will tell you what the result would be. They can put those events together in their minds, and argue from them that something will come to pass. There are few people, however, who, if you told them a result, would be able to evolve from their own inner consciousness what the steps were which led up to that result. This power is what I mean when I talk of reasoning backwards.”
No matter how many facts are at our disposal, how capacious and deep our memory might be (and there are people whose talent in memorization is staggering), it is useless unless we know how and what to apply to a particular situation. In fact, the “what” is a major component of the “how.”
While most people observe “causes” and infer the “results” that will follow, Holmes prides himself in being able to start with the “results” and reason his way backwards to their original “causes.”
In the knowledge diffusion process, adsorption involves preferential partitioning (of substances) onto the surface, model for the behavior of a large set of coupled oscillators.
This architecture is a mathematical model used in describing orchestration of multiple dynamic sequences and subsequences – we called it Dynamic Algebraic Cognitive Subsequence or DACS. More specifically, it is a model for the behavior of a large set of coupled oscillators.
Although it is conceptually extremely simple, in captures the basic mechanism of spontaneous orchestration of interacting oscillators, it explains why orchestration sometimes occurs and sometimes doesn’t. Despite it is formal simplicity it holds a number of unexpected surprises when many oscillators are involved, such as the coexistence of coherent and incoherent dynamics – also known as chimera state. It is surprising that this behavior occurs in symmetrically coupled identical oscillators.
First, let’s discuss about oscillators. The defining features of an oscillator is the repetition of behavior. So we have a dynamic state of the system that repeats and repeats and repeats. Nature abounds in processes that are oscillatory, rhythmic or repetitive. Geometrically you can think of the periodic motion as curve in the NN-dimensional state space. This geometric idea is very helpful. Because it means that we can geometrically map the periodic trajectory, even if it looks complicated and potentially with a weird shape in state space onto a nicely shape circle, with every point on the periodic trajectory corresponding to a point on the circle. Just like we can have a rubber-band shaped in weird ways to be reshaped into a nice circular shape. No matter what weird shape the rubber band is in, it remains a circular object.
Second, the process known as adsorption, which involves nothing more than the preferential partitioning of substances (from the gaseous or liquid phase) onto the surface of a solid substrate, for example, from the early days of using bone char for decolorization of sugar solutions and other foods. In structuring machine learning, the process of adsorption involves separation of a content (audio, video, cognitive, context) from one phase accompanied by its accumulation or concentration at the surface of another. In short, adsorption is a consequence and/or subsequence of State, Action, Response, Reward – in SCANN – that represent surface energy.
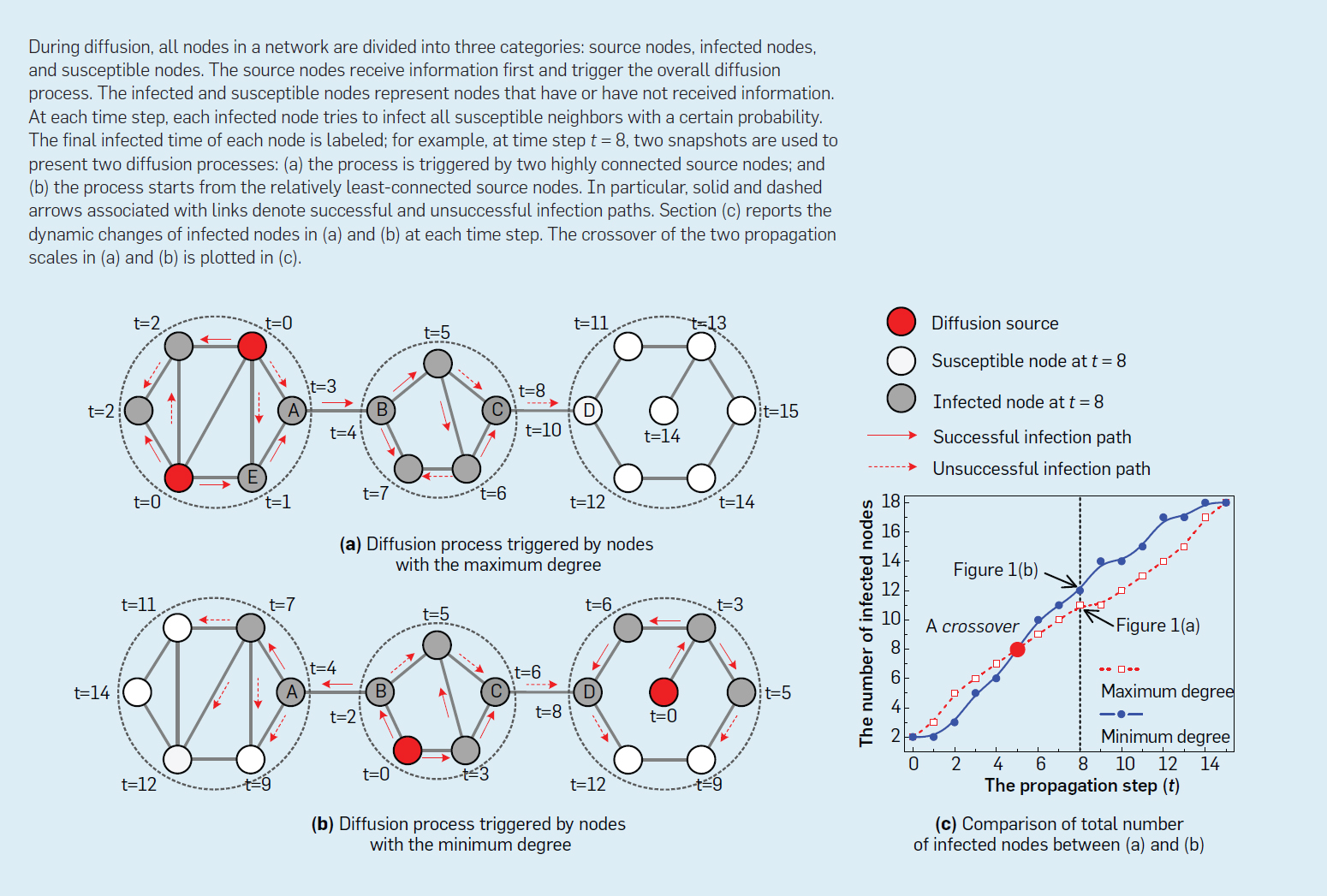
Third, the process of diffusion in the knowledge sharing or diffusion that takes place over network structures and as a mechanism of network creation – a fundamental aspect of the economic activity. This formulates the effect of trade in an endogenous growth model – phase transitions – in which comparative advantage and the stock of knowledge are determined by innovation and diffusion. A Diffusion-Limited Aggregate (DLA) is a process in which particles (knowledge of humans or machines) undergo random motion due to Brownian motion and are allowed to cluster together forming a fractal structure. This is applicable to aggregation in any system where diffusion is the primary means of transport in the system.
So, bottom-line: An adsorption-oscillator is described, abstractly, as an angle variable theta(t) or θ(t) that moves around a circle within a given phase. It doesn’t have to do it at a constant speed. In some circle regions it could move faster than in others. It could even come to a stop (stretching the idea of an oscillator a bit).
Because we have this motion on a circle, it also means that the motion has no beginning and no end. If we want to measure the state, and attach a number to it, we need to set a point on the circle that corresponds to theta=0 or θ=0, as mentioned earlier. If we embed the circle in the plane with our conventional placement of x– and y-axis, the beginning is usually placed at the cartesian point (1,0) and increasing theta (θ) is happening in the counter-clockwise way. It is a convention to define the angle with respect to the x-axis and increasing the angle means moving the state in a counter-clockwise fashion. Pure convention. You could start anywhere and move in any direction.
Naturally, the next step is considering many coupled diffusion-adsorption-oscillators (“oscillators”). The generalization of the two-oscillator model comes naturally. We just assume that any pair of oscillators exert a force on each other that is identical to the two-oscillator system. This illustrates pattern formation, interesting and beautiful properties of oscillators that are spatially arranged on a lattice and interact with their neighbors. Oscillators and their interaction are for phase coupled oscillators. The model is amazing, because on one hand it is conceptually quite simple, on the other it holds a number of unexpected dynamical secrets that one can discover here.
An important goal of oscillator network is to identify how (i) individual oscillator’s dynamics, (ii) network topology and (iii) coupling type conspire to create emergent spatio-temporal patterns in the form of steady phase relationships between oscillators. Addressing this fundamental goal has motivated the development of controlled experimental systems that operate with varying degrees of autonomy.
“You do occasionally find a carrion crow among the eagles,” Holmes tells Watson in “Shoscombe Old Place,” using an avian metaphor to describe the possibility that Sir Robert Norberton is a bad ‘un. It’s not a kind way to speak of crows, who by all informed accounts are highly intelligent and social creatures, but he said it and we have to deal with it. The mystery of 221B Baker Street is not one of secret passages or hidden symbols. Rather, it could be described as a sort of existential spatial riddle: how can a space that is not a space be where it is not? Penned by Conan Doyle “I consider that a man’s brain originally is like a little empty attic, and you have to stock it with such furniture as you choose. A fool takes in all the lumber of every sort that he comes across, so that the knowledge which might be useful to him gets crowded out, or at best is jumbled up with a lot of other things, so that he has a difficulty in laying his hands upon it. Now the skillful workman is very careful indeed as to what he takes into his brain-attic. He will have nothing but the tools which may help him in doing his work, but of these he has a large assortment, and all in the most perfect order. It is a mistake to think that that little room has elastic walls and can distend to any extent. Depend upon it there comes a time when for every addition of knowledge you forget something that you knew before. It is of the highest importance, therefore, not to have useless facts elbowing out the useful ones.”
[A Study in Scarlet (1887)]
