An effective method for designing neural network that derives the stages in-between proactive and retroactive learning in two different time points is to classify patterns in the multi-dimensional feature space. This deep learning architecture introduces a multi-dimensional feature space where the information waits in certain workspace – the Voronoi region – within the neural network based on distance to points in a specific subset of the plane. The Voronoi diagram is derived over points in feature space which represents teachers’ input in order to realize the desired classification. However, to reduce the size of the neural network and make the learning efficient, clustering procedure that enables the subject to manage a number of teachers in a lump is implemented. Our approaches, however, only utilize point-wise cell-membership – as new information – by means of nearest-neighbor queries and do not utilize further geometric information about Voronoi cells since the computation of Voronoi diagrams is prohibitively expensive in high dimensions. Therefore, a Monte-Carlo-Markov-Chain integration-based approach that computes a weighted integral over the boundaries of Voronoi cells, thus incorporates additional information – as retroactive confirmation – about the Voronoi cell structure is established. This dynamic proactive- retroactive learning method predicts and prescribes an action in “expected” response to an activity of human (or interchangeably a machine), depending on individual’s state, for one or more end-rewards, or pay-offs at a given point in time.

Since most information related to immediate relevance including dynamic active cognitive state and/or active experiences, hence individuals apply a certain set of rules that are associated with either sequential monadic (e.g., individual’s state from a to 𝑎́ as self-improvement) or paired-comparison (e.g., individual’s state x compared with another individual’s state y) with nearest neighbor or a group where individual is a member. This, in imperfect or asymmetric and incomplete information conditions, creates “hidden” multi-layered combinations on multi-dimensions – functional, non-functional, non- discriminating and discriminating – features to predict and determine the cognitive state (or “state”). The group, where individual is a member, may also apply a certain set of collective “hidden” information associated with either linear-non-linear (e.g., a race-car driver uses wind direction data while cornering at speeds more than 200 mph without informing the opponent. Another example, kids learn how to ride a bicycle) or paired comparison (e.g. race car the team analyzes data of other racers’ degradation rates on the tires and of the health of various mechanical components, and recording the drivers’ steering, braking and throttle inputs. Another example a teacher often struggles to make his or her student how to play a piano. The student also has to learn – as ‘self-organized’ – to play with correct technique or could face injuries in the future). In imperfect and incomplete information conditions, this generates aggregated “hidden” multi-layered combinations on multi-dimensions features to predict and determine a collective state.

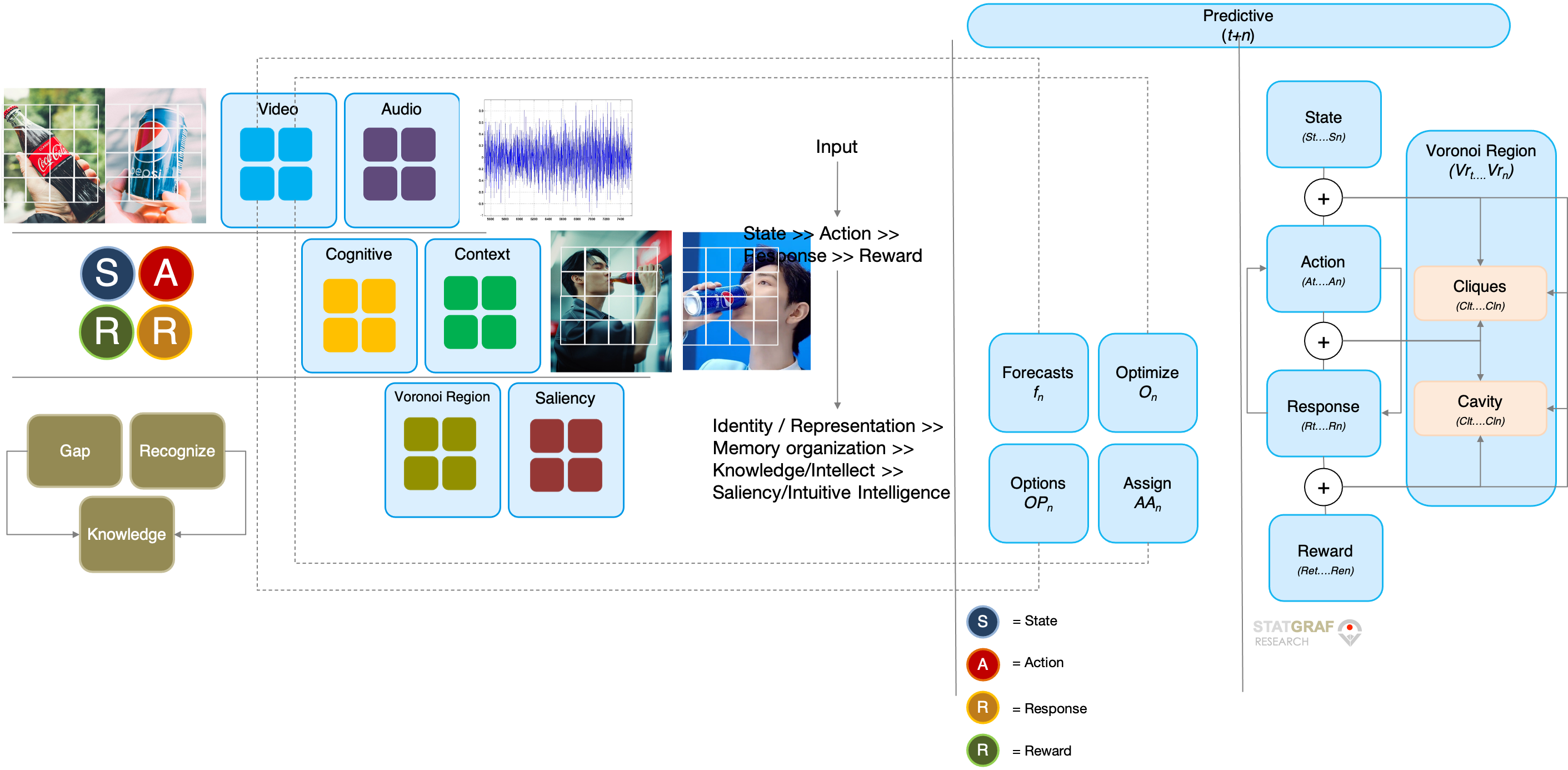
For some combinatorial problems, where all rules and information are known to all parties, one may set up intermediate positions for them to achieve the optimal results where, as in real-life conditions, such learning success depends on how well one would fragment a “major” decision or an objective into a series of multiple “smaller” decisions – the decision journey – and actions to measure their progress accurately.

To understand these interactions and to elicit deep-seated knowledge held by humans, researchers for long used the “Projective techniques” – projection of humans – for inferring about underline motives, opinions, beliefs or intentions on other people or even objects, which cannot be secure through direct questioning as the respondent either resists to reveal them or is unable to figure out himself. In addition, researcher formulated tools for accessing sub-conscious needs, motivations, attitudes and perceptions.

Projection where it referred to the inherent capacity of neurons to transmit stimuli from one level of the nervous system to another (e.g., the retina “projects” to the occipital cortex, where raw sensory input is rendered into visual images). Projection, the mental process by which people attribute to others what is in their own minds. For example, individuals who are in a self-critical state, consciously or unconsciously, may think that other people are critical of them.

In projection, what is internal is seen as external. People cannot get inside the minds of others; to understand someone else’s mental life, one must project one’s own experience. When someone projects what is consciously true of the self and when the projection “fits,” the person who is the object of projection may feel deeply understood. Thus, a sensitive father infers from his daughter’s facial expression that she is feeling sad; he knows that when he himself is sad, his face is similar. If he names the child’s assumed emotion, she may feel recognized and comforted. Intuition, leaps of non-verbal synchronicity (as when two persons in a relationship suddenly find themselves making similar gestures or thinking of the same image simultaneously), and peak experiences of mystical union (as when one feels perfectly attuned with an idealized other person, such as a romantic partner) involve a projection of the self into the other, often with powerful emotional rewards. Neuroscientific discoveries regarding mirror neurons and brain-to-brain communication processes (in which intuitive, emotional, nonverbal, and analogical thinking is shared between caregivers and children via intonation, facial affect, and body language) are establishing the neurological bases of such long-noted projective phenomena.

The power of combing representational techniques to communicate multiple aspects of an activity. An axonometric view and a section perspective work in tandem to communicate the exterior façade’s as well as the interior knowledge within them. The two parallel projections are unusual in different ways — the first rotates the entire oscillator in space to provide a ground-up (or inner) view, which presents the activity from a believable human viewpoint. The second provides us with a birds-eye (or outer) view, showing the multi-level “smaller” activities that allow humans to enter throughout the activity.

Projected graphs, or subgraphs in mathematical terms, are graphs with an edge set and a vertex set belonging to a subset of an edge set and a vertex set of another graph. In plane projections, a series of points on one plane may be projected onto a second plane by choosing any focal point, or origin, and constructing lines from that origin that pass through the points on the first plane and impinge upon the second. Such projective geometry deals with the relationships between geometric figures and the images, or mappings, that result from projecting them onto another surface. Common examples of projections are the shadows cast by opaque objects and motion pictures displayed on a screen. A second common type of projection is called stereographic projection. It refers to the projection of points from a sphere to a plane. This may be accomplished most simply by choosing a plane through the centre of the sphere and projecting the points on its surface along normal, or perpendicular lines, to that plane. 

A set of networks whose nodes are divided into two sets X and Y, and only connections between two nodes in different sets are allowed, could be bipartite networks. For the convenience of directly showing the relation structure among a particular set of nodes, bipartite networks are usually compressed by projection – also referred as bipartite network projection.  Bipartite networks are the natural representation for several systems, such as: social affiliation and collaboration networks, where individuals connect to the groups they are member of; financial and commercial ownership networks, where entities are linked to the goods or services they own or consume; trade networks, where economies connect to the products they export; ecological networks, where species connect to the habitat they live in; biological and medical networks connecting, e.g., patients and diseases. Multipartite networks are an example in which various scenarios are represented by different types of relations, actors, or modes. Within this context, the present contribution aims at discussing an analytic strategy for simplifying multipartite networks in which different sets of nodes are linked. By considering the connection of multimode networks and hypergraphs as theoretical concepts, a three-step procedure is introduced to simplify, normalize, and filter network data structures. Thus, a model-based approach is introduced for derived bipartite weighted networks in order to extract statistically significant links.

Synchronization is perhaps the most cross-disciplinary concept of emergence of collective behavior as it is manifested across many branches of natural and social sciences. Ensembles of neurons, fireflies or humans are prone to synchronize their internal rhythms when they become coupled enough, producing a macroscopic dynamically coherent state. The study of network synchronization has found application in many areas of science and technology and many of the networks studied in this context frequently fall in the bipartite class. In the such conditions, each node corresponds to an oscillator and the signal transmission in the system is subject to a time delay τ . The observation that oscillators 1 and 3 can be perfectly phase synchronized while oscillators 1 and 2 and oscillators 2 and 3 are lag synchronized is an example of the interesting spatio-temporal behavior that can arise in relay-coupled bipartite systems. This also underscores the importance of understanding synchronized solutions (both in-phase and antiphase) as a mechanism for bringing about complex temporal correlations in spatially extended systems. Our intent is to design in the nature of synchronization of oscillators on multipartite networks when there is an inherent delay in the coupling. A widely adopted model of a coupled oscillator network is characterized by a population of phase oscillators, a graph describing the interaction among them, and diffusive and sinusoidal coupling. It is known that a strongly coupled and sufficiently homogeneous network synchronizes, but the exact threshold from incoherence to synchrony is unknown.